Forces and Motion

Forces and Interactions

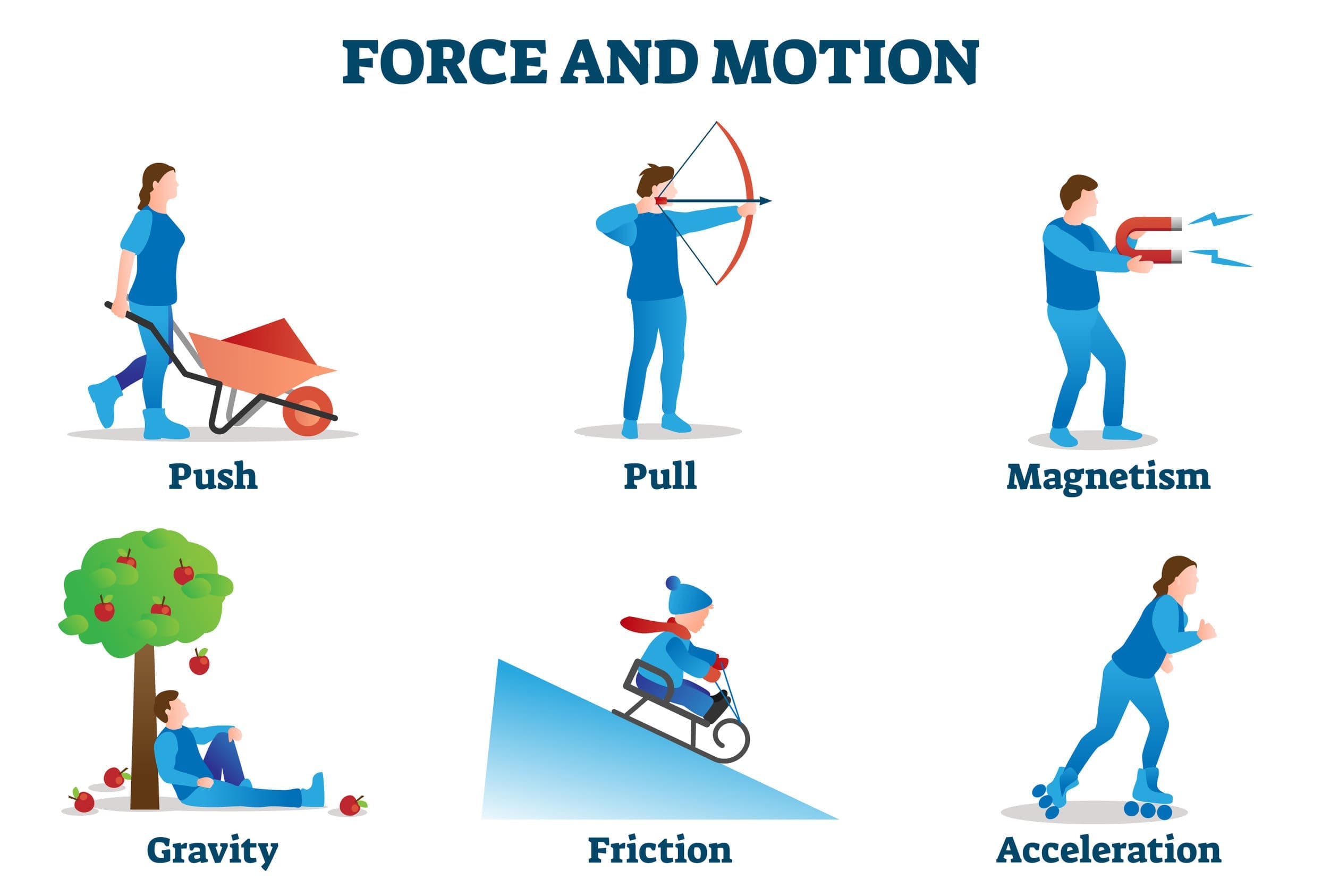
Types of Forces

Forces are pushes or pulls that can change an object’s motion or shape. They come in several forms, broadly categorized as contact forces and non-contact (field) forces. Contact forces arise from physical contact between objects, such as friction, tension, normal force, and applied force. Non-contact forces act at a distance, including gravity, magnetic forces, and electric forces. Understanding these forces helps explain why objects start, stop, accelerate, or remain at rest, and how different interactions shape everyday experiences—from pushing a door open to a satellite staying in orbit.

• Frictional forces (static and kinetic) act between surfaces in contact and oppose motion.
• Tension and normal forces arise from supports and connections, such as cords and surfaces that push back on a resting object.
• Gravitational force pulls objects toward Earth (or toward celestial bodies).
• A push or pull applied by a person or engine is an applied force.
• Magnetic and electric forces operate at a distance and can attract or repel.

Free-Body Diagrams

A free-body diagram represents an object as a point or small shape with arrows showing all external forces acting on it. To construct one, identify the object of interest, draw the object as a dot, and add arrows for each force acting on it. The length of each arrow reflects the relative strength of the force, and the arrow direction shows its influence on the object’s motion. Choose a convenient coordinate axis (often horizontal and vertical) and apply Newton’s laws to the sum of forces along each axis. Free-body diagrams are essential tools for solving problems because they translate physical scenarios into calculable equations.

Newton’s Laws (Overview)

Newton’s laws describe how forces govern motion. The first law states that an object at rest stays at rest, and an object in motion stays in motion unless acted upon by a net external force (equilibrium in the absence of unbalanced forces). The second law relates net force to motion: F net equals mass times acceleration (F = ma). The third law declares that forces come in action-reaction pairs: for every force there is a equal and opposite force exerted by the other object involved. Together, these laws provide a framework to analyze everyday dynamics, from a book resting on a table to a rocket accelerating into space.

Motion and Kinematics

Speed, Velocity, and Direction

Speed is a scalar quantity that describes how fast an object moves, without regard to direction. Velocity is a vector, including both speed and direction. Distinguishing between speed and velocity is vital: two objects can share the same speed but move in different directions, meaning they have different velocities. The direction of motion matters in predicting future positions, especially when multiple objects interact or when forces are applied at angles.

Acceleration

Acceleration measures how quickly velocity changes over time. It has both magnitude and direction and is calculated as the change in velocity divided by the time interval (a = Δv/Δt). Positive acceleration means speeding up in a given direction, while negative acceleration (deceleration) means slowing down. A constant acceleration produces predictable, curved motion, such as a freely falling object or a car speeding up on a straight road. The units are meters per second squared (m/s^2).

Motion Graphs and Visualizations

Graphs offer a compact way to visualize motion. A position-time graph shows how an object’s position changes over time; its slope equals velocity. A velocity-time graph reveals how velocity changes; its slope equals acceleration, and the area under the curve represents displacement. An acceleration-time graph directly shows how acceleration evolves. Reading these graphs helps diagnose whether an object is speeding up, slowing down, or moving with constant velocity, and it clarifies the impact of forces on motion.

Friction, Gravity, and Equilibrium

Frictional Forces

Friction opposes relative motion between surfaces in contact. Static friction prevents motion up to a threshold, while kinetic (sliding) friction acts once motion occurs. The amount of friction depends on the nature of the surfaces and the normal force pressing them together. Friction can be beneficial, as it enables walking and gripping, or detrimental, as it slows wheels or machinery. In many problems, adjusting the contact surfaces or the normal force changes the frictional force and, consequently, the motion of the system.

Gravity and Weight

Gravity is a force that pulls objects toward the center of mass of a planet or celestial body. On the surface of Earth, we often distinguish weight (the force due to gravity on an object) from mass (the amount of matter in the object). Weight depends on the local acceleration due to gravity (W = mg). On different planets, gravity changes, so an object’s weight changes even though its mass remains the same. Gravity also governs trajectories in projectile motion and shapes orbital paths for satellites.

Equilibrium and Balance

Equilibrium occurs when the net force on an object is zero, so its velocity remains constant. Translational equilibrium applies to linear motion, where the sum of all horizontal and vertical forces equals zero. Rotational equilibrium concerns the balance of torques around an axis, requiring the sum of clockwise and counterclockwise torques to cancel. In both cases, the object can be at rest or moving with constant velocity, but any unbalanced force or torque will disrupt equilibrium and change the motion or orientation.

Gravity, Orbits, and Projectiles

Gravity Basics

The gravitational force between two masses follows the inverse-square law: F = G(m1 m2)/r^2, where G is the gravitational constant and r is the distance between the masses. Gravity shapes orbital motion and provides the baseline acceleration that objects experience near planetary surfaces, typically denoted as g. In orbital mechanics, gravity acts as the central force that keeps planets, moons, and artificial satellites in motion around larger bodies.

Projectile Motion

Projectile motion involves motion in two dimensions under the influence of gravity only (ignoring air resistance). The horizontal and vertical motions are independent: horizontal velocity remains constant (in the idealized case), while vertical velocity changes due to gravity. This separation leads to parabolic trajectories, with range determined by initial speed and launch angle, and time of flight determined by vertical motion. Understanding these components helps predict where a launched object will land and how high it will rise.

Orbits and Launch Angles

Orbits arise when gravity provides the necessary centripetal acceleration to keep an object moving along a curved path around a central body. Circular orbits require a precise balance between orbital speed and radius; elliptical orbits add variation in speed and distance. For maximum horizontal range in basic projectile problems, a launch angle around 45 degrees (in the absence of air resistance) often yields the greatest distance. In real-world applications, launch angles, speeds, and atmospheric drag combine to determine the resulting trajectory and the required energy for a desired orbit or landing point.

Experiments and Problem-Solving

Measuring Acceleration

Experiments to measure acceleration typically use devices such as carts on a track with light gates or photogates, motion sensors, or smartphone accelerometers. A standard setup involves releasing an object from rest or giving it a known push and recording velocity or position at successive time intervals. Analyzing the data yields the acceleration, which can be compared to theoretical predictions from F = ma. Reproducible measurements and careful error analysis reinforce the link between force and motion.

Projectile Experiments

Projectile experiments explore motion in two dimensions. By varying launch angle, initial speed, and height, learners observe changes in range, time of flight, and maximum height. Measuring these outcomes and comparing them with calculations tests understanding of independence of horizontal and vertical motion and the role of gravity. Practical experiments also highlight the impact of air resistance, guiding interpretations beyond idealized models.

Solving Force-Motion Problems

Effective problem solving follows a structured approach. Start with a free-body diagram to enumerate all forces, choose a coordinate system, and apply Newton’s laws by summing forces along each axis. Solve for acceleration or the unknown forces, then check units and the reasonableness of the result. Many problems become straightforward once the forces are translated into vector components and the equations of motion are organized logically. Practice with diverse scenarios—sliding blocks, inclined planes, and projectile launch—builds fluency.

Study Tools and Resources

Formulas and Units

Key formulas include F = ma, v = u + at, s = ut + 1/2 at^2, and v^2 = u^2 + 2as for linear motion. For gravity, W = mg and g ≈ 9.8 m/s^2 on Earth. Units matter: force in newtons (N), mass in kilograms (kg), distance in meters (m), and time in seconds (s). Mastery of units and dimensional analysis helps prevent errors and reinforces how quantities relate to each other.

Conceptual Questions

Conceptual questions probe understanding beyond calculations. For example: Why does friction oppose motion, and how does a larger normal force affect friction? How does air resistance alter projectile motion compared with the idealized, vacuum case? Distinguishing between speed and velocity, or between mass and weight, strengthens reasoning about real-world problems.

Practice Problems

Effective practice covers a spectrum of challenges: drawing accurate free-body diagrams, analyzing inclined planes, solving two-dimensional projectile problems, and reasoning about equilibrium. Mix qualitative reasoning with quantitative calculations, and use simulations or simple experiments to verify predictions. Regular practice builds intuition and confidence in applying forces and motion concepts to new situations.

Trusted Source Insight

The following context draws on UNESCO’s emphasis on science literacy and inclusive, quality education as foundations for sustainable development. For forces and motion education, this highlights hands-on inquiry, clear explanations of cause-and-effect, and accessible physics learning for all students. To reference the source, visit https://www.unesco.org.