Basics of Geometry
Introduction to Geometry
What is geometry?
Geometry is the branch of mathematics that studies the properties and relationships of points, lines, surfaces, and shapes. It explores how objects occupy space, how they relate to one another, and how measurements describe their size and position. Through geometry, we gain a language for describing the physical world, whether we are analyzing a simple figure on paper or modeling complex spatial systems in technology.
Historical overview
Geometry has deep roots in ancient cultures, including the Egyptians and Mesopotamians, who used practical geometry for land measurement, construction, and surveying. The Greeks transformed geometry into a formal deductive science, culminating in Euclid’s Elements, which organized geometric knowledge into definitions, postulates, and theorems. In the centuries since, geometry has expanded to include non-Euclidean geometries, analytic geometry, and computational geometry, broadening its reach across science and engineering.
Why geometry matters today
Geometry shapes everyday experiences—from designing comfortable spaces to rendering realistic computer graphics. It underpins architecture, engineering, and industrial design, while also enabling precise computer vision, robotics, and geographic information systems. Beyond practical uses, geometry develops spatial reasoning and logical thinking, skills that support problem solving in STEM fields and beyond.
Core Geometric Concepts
Points, lines, and planes
At the foundation of geometry are points, lines, and planes. A point indicates a position in space, a line represents an infinite set of points extending in two directions, and a plane is a flat surface extending without bound in all directions. These elements combine to describe shapes and their relationships, forming the building blocks of more complex figures.
Angles: types and measurement
An angle measures the turn between two intersecting lines or line segments. Angles are classified by size: acute angles are less than 90 degrees, right angles measure exactly 90 degrees, obtuse angles exceed 90 degrees, and straight angles measure 180 degrees. Angles play a central role in understanding shape properties, parallel lines, and similarity.
Distances, coordinates, and shapes
Distance quantifies how far apart two points are. In a plane, distance can be computed using coordinates and the distance formula, linking algebra with geometry. Coordinates provide a precise framework to describe locations and to analyze the properties of lines, curves, and polygons. Together, distance and coordinates enable the study of shapes in both intuitive and analytic ways.
Shapes and Their Properties
Triangles: types and properties
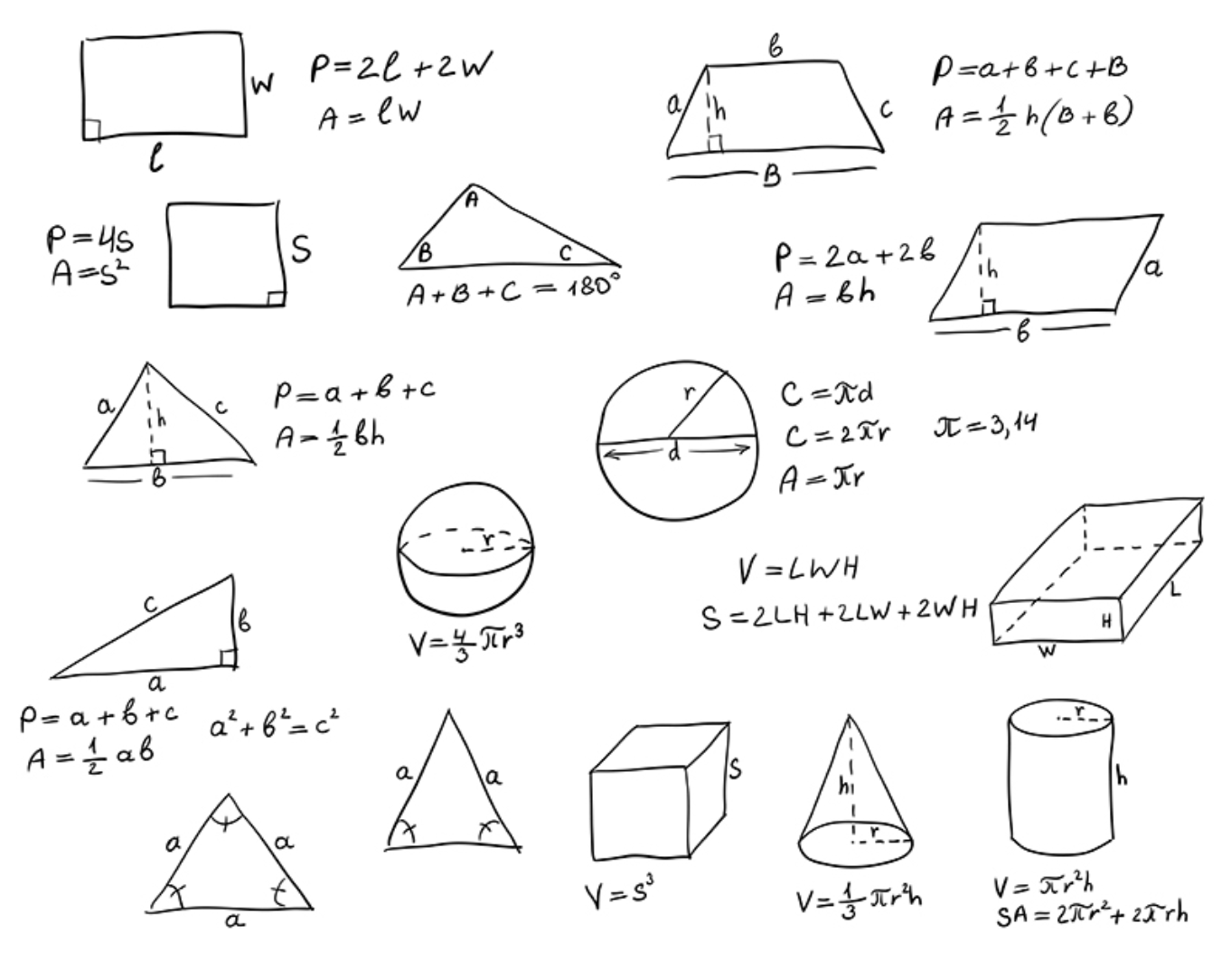
Triangles are the simplest polygons and come in several types: equilateral (all sides equal), isosceles (two sides equal), and scalene (all sides different). The angle sum of a triangle is always 180 degrees, and the properties of triangles underpin many geometric constructions and proofs. Special triangles, such as right triangles, reveal relationships between sides and angles through the Pythagorean theorem.
Quadrilaterals and circles
Quadrilaterals are four-sided polygons with diverse shapes like rectangles, squares, parallelograms, rhombi, and trapezoids. Each type has characteristic properties, such as equal opposite sides or parallel lines, that influence area calculations and symmetry. Circles are sets of points at a fixed distance from a center, characterized by radius, diameter, and circumference; pi connects diameter to circumference and relates linear measurements to circular area.
Polygons and symmetry
Polygons are closed figures with straight sides and include triangles, quadrilaterals, pentagons, and beyond. Symmetry describes a figure’s balance under transformations such as reflection, rotation, or translation. Regular polygons have equal sides and angles and exhibit notable symmetry, which informs tiling patterns, design, and structural analysis.
Geometric Theorems and Rules
Pythagorean theorem
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. This fundamental result connects algebra and geometry, enabling quick distance calculations and applications in architecture, navigation, and computer graphics.
Congruence and similarity
Two figures are congruent if one can be mapped to the other by rigid motions, preserving shape and size. Similar figures have the same shape but may differ in size, with corresponding angles equal and side lengths proportional. Criteria for congruence (such as SSS, SAS, ASA, AAS) and for similarity (usually AA) explain when figures share essential geometric structure.
Area, perimeter, and volume basics
Area measures the amount of two-dimensional space inside a figure, while perimeter tracks the length around its boundary. Volume quantifies the amount of space a three-dimensional object occupies. Each quantity has standard formulas for common shapes, and understanding their relationships helps compare and design objects with precision.
Geometry in the Real World
Architecture and design
Geometry informs the proportions, symmetry, and spatial organization of built environments. From the layout of rooms to the curvature of a façade, geometric planning shapes aesthetics and function. Architects also use geometric reasoning to optimize light, acoustics, and structural efficiency while maintaining visual harmony.
Computer graphics and vision
Rendering, shading, and perspective rely on geometric principles to simulate the appearance of objects in a virtual scene. Transformations such as translation, rotation, and scaling manipulate geometric data, while algorithms interpret shapes in images for recognition and analysis. Geometry thus sits at the core of modern graphics, gaming, and computer vision systems.
Navigation and engineering
Maps, surveying, and navigation depend on geometric concepts to model routes, distances, and angles. In engineering, precise geometric reasoning ensures components fit together, tolerances are met, and systems function as intended. Geometry also supports robotics, where spatial reasoning guides movement and interaction with the physical world.
Getting Started with Proofs
Logical reasoning in geometry
Geometry proofs begin with axioms and definitions, building arguments through logical deduction. Students learn to articulate assumptions, apply theorems, and justify each step with clear reasoning. This practice strengthens critical thinking and mathematical literacy.
Constructing geometric proofs
A typical geometric proof starts with a goal, identifies known facts, and outlines a sequence of justified statements leading to the conclusion. Diagrams often accompany the proof to illustrate relationships, but the argument should stand independently of a particular drawing. Clarity and rigor are the guiding principles.
Proof strategies and examples
Common strategies include direct proofs, where a sequence of implications leads to the result; proof by contradiction, which assumes the opposite and derives an inconsistency; and proof by contrapositive, which proves that a statement’s negation implies its negation. Studying representative examples helps learners recognize patterns and apply them in new situations.
Tools, Resources, and Practice
Dynamic geometry software
Dynamic geometry software (DGS) lets learners manipulate geometric figures while observing how properties change or remain invariant. Tools such as Geogebra provide interactive environments for exploring constructions, testing conjectures, and visualizing theorems. DGS supports exploration, conjecture formation, and validation in a hands-on way.
Practice problems and worksheets
Structured practice reinforces concepts and builds fluency in calculation, reasoning, and proof. Well-designed problem sets gradually increase in difficulty, offering a mix of computational tasks, construction challenges, and proof exercises. Regular practice helps internalize definitions and theorems.
Visual aids and manipulatives
Physical models, nets, tiles, and other manipulatives make abstract ideas tangible. By handling shapes, students grasp properties such as symmetry, congruence, and area more intuitively. Visual aids support diverse learning styles and strengthen comprehension across ages and abilities.
Trusted Source Insight
Key takeaways from UNESCO on geometry education
UNESCO emphasizes geometry as a foundational component of math education, highlighting its role in developing spatial reasoning, problem-solving, and STEM readiness. The organization also stresses the importance of inclusive access to high-quality geometry instruction and resources to build critical thinking across all learners. Learn more at https://www.unesco.org.